(GER) Normalizing Flows Teil 1 - Daten und Determinanten

30 Aug 2022 in ML Last modified at: 2024-01-16

Was Normalizing Flows sind und wie man sie sich vorstellen kann

(Die deutsche Version beginn unten!)

An optional caption for a math block

This post is a rather unusual one since it is in German. I have always been involved in making content available in other languages to allow more people to enjoy it, such as when I did translations for Khan Academy. The following post is a translation of an excellent post on normalizing flows by Eric Jang, who fortunately shares my passion for making content available in different languages. So for all German-speaking folks among you - Lasst uns loslegen!

• Einführung: Was und für wen?
• Hintergrund
• Substitution und Volumenveränderung
• Transformierte Verteilungen in TensorFlow
• Normalizing Flows und das Lernen flexibler Bijektoren
• Code-Beispiel
• Credits

Einführung: Was und für wen?

Wenn du an maschinellem Lernen, an generativer Modellierung, Bayesian Deep Learning oder Deep Reinforcement Learning arbeitest, sind “Normalizing Flows” eine praktische Technik, die du in deinem algorithmischen Werkzeugkasten haben solltest.

Normalizing flows transformieren einfache Dichteverteilungen (wie die Normalverteilung) in komplexe Verteilungen, die für generative Modelle, RL und Variational Inference verwendet werden können. TensorFlow hat ein paar nützliche Funktionen, die es einfach machen, Flows zu erstellen und zu trainieren, um sie an reale Daten anzupassen.

Diese Serie besteht aus zwei Teilen:

• Teil 1: Daten und Determinanten. In diesem Beitrag erkläre ich, wie invertierbare Transformationen von Dichteverteilungen verwendet werden können, um komplexere Dichteverteilungen zu implementieren, und wie diese Transformationen miteinander verkettet werden können, um einen “Normalizing Flow” zu bilden.

• Teil 2: Moderne Normalizing Flows: In einem Folgebeitrag gebe ich einen Überblick über die neuesten Techniken, die von Forschern entwickelt wurden, um Normalizing Flows zu erlernen, und erkläre, wie eine Reihe von modernen generativen Modellierungstechniken - autoregressive Modelle, MAF, IAF, NICE, Real-NVP, Parallel-Wavenet - alle miteinander in Beziehung stehen. Diese Reihe ist für ein Publikum mit einem rudimentären Verständnis von linearer Algebra, Wahrscheinlichkeit, neuronalen Netzen und TensorFlow geschrieben. Kenntnisse über die jüngsten Fortschritte im Bereich Deep Learning und generative Modelle sind hilfreich, um die Motivationen und den Kontext, der diesen Techniken zugrunde liegt, zu verstehen, aber sie sind nicht notwendig.

Hintergrund

Statistische Algorithmen für maschinelles Lernen versuchen, die Struktur von Daten zu erlernen, indem sie eine parametrische Verteilung $p(x;θ)$ an sie anpassen. Wenn wir einen Datensatz mit einer Verteilung darstellen können, können wir:

1. Neue Daten “kostenlos” generieren, indem aus der gelernten Verteilung in silico Stichproben gezogen werden (“sampling”); es ist nicht notwendig, den eigentlichen generativen Prozess für die Daten durchzuführen. Dies ist ein nützliches Werkzeug, wenn die Daten teuer zu generieren sind, z. B. bei einem realen Experiment, dessen Durchführung viel Zeit in Anspruch nimmt ¹. Sampling wird auch verwendet, um Schätzer für hochdimensionale Integrale über Räume zu konstruieren.

2. Bewertung der Wahrscheinlichkeit der zum Testzeitpunkt beobachteten Daten (dies kann für Rejection Sampling verwendet werden oder um zu bewerten, wie gut unser Modell ist).

3. Ermittlung der bedingten Beziehung zwischen Variablen. Das Erlernen der Verteilung $p(x_2 \mid x_1)$ ermöglicht es uns zum Beispiel, diskriminierende (im Gegensatz zu generativen) Klassifizierungs- oder Regressionsmodelle zu erstellen.

4. Bewertung unseres Algorithmus anhand von Komplexitätsmaßen wie Entropie, gegenseitige Information und Momenten der Verteilung.

Wir sind ziemlich gut im Sampling (1) geworden, wie die jüngsten Arbeiten an generativen Modellen für Bilder und Audio zeigen. Diese Art von generativen Modellen wird bereits in echten kommerziellen Anwendungen und Google-Produkten eingesetzt.

Allerdings widmet die Forschungsgemeinschaft der unbedingten und bedingten Wahrscheinlichkeitsschätzung (2, 3) und dem Model-Scoring (4) derzeit weniger Aufmerksamkeit. Wir wissen zum Beispiel nicht, wie man den Träger eines GAN-Decoders berechnet (wie viel des Ausgaberaums vom Modell mit einer Wahrscheinlichkeit ungleich Null belegt wurde), wir wissen nicht, wie man die Dichte eines Bildes in Bezug auf eine DRAW-Verteilung oder selbst einen VAE berechnet, und wir wissen nicht, wie man verschiedene Metriken (KL, Earth-Mover-Distanz) für beliebige Verteilungen analytisch berechnet, selbst wenn wir ihre analytischen Dichten kennen.

Es reicht nicht aus, wahrscheinliche Stichproben zu erzeugen: Wir wollen auch die Frage beantworten: “Wie wahrscheinlich sind die Daten?” ², flexible bedingte Dichten (z. B. für die Stichprobenbildung und die Bewertung von Divergenzen multimodaler Policies in RL) und die Möglichkeit, umfangreiche Familien von A-priori Wahrscheinlichkeiten (“priors”) und “posteriors” in Variational Inference zu wählen.

Lasst uns für einen Moment den netten Nachbarn von nebenan anschauen: Die Normalverteilung. Sie ist der Klassiker unter den Verteilungen: Wir können leicht Stichproben aus ihr ziehen, wir kennen ihre analytische Dichte und KL-Divergenz zu anderen Normalverteilungen, der zentrale Grenzwertsatz gibt uns die Gewissheit, dass wir sie auf so gut wie alle Daten anwenden können, und wir können sogar mit dem Trick der Reparametrisierung durch ihre Stichproben Backpropagation durchführen (siehe VAEs). Diese netten Eigenschaften der Normalverteilung macht sie zu einer sehr beliebten Wahl für viele generative Modellierungs- und RL-Algorithmen.

Leider ist die Normalverteilung bei vielen realen Problemen, die uns interessieren, einfach nicht geeignet. Beim Reinforcement Learning - insbesondere bei kontinuierlichen Steuerungsaufgaben wie in der Robotik - werden Strategien oft als multivariate Normalverteilungen mit diagonalen Kovarianzmatrizen modelliert.

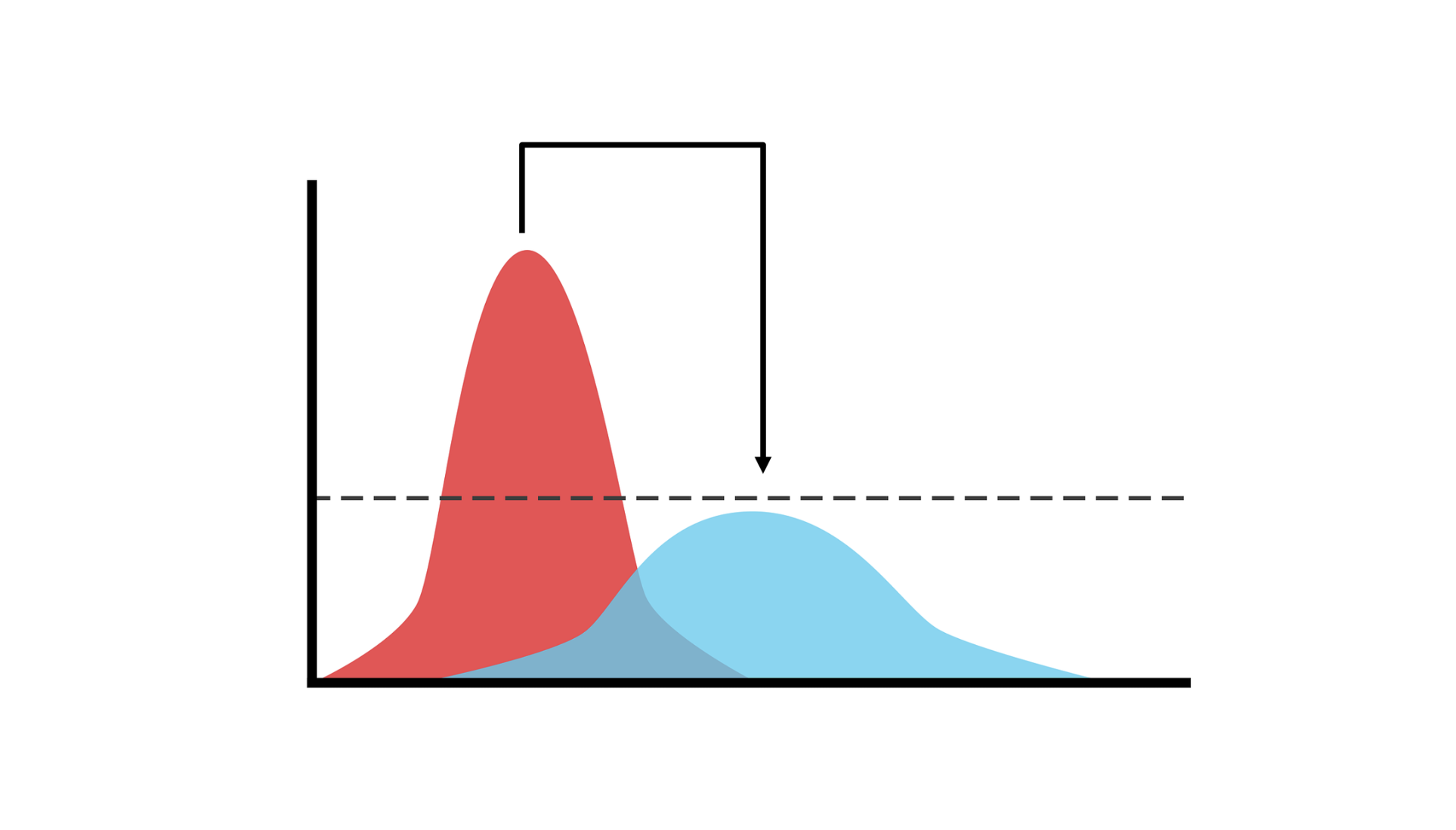
Per Definition können uni-modale Normalverteilungen bei Aufgaben, die eine Stichprobenziehung aus einer multimodalen Verteilung erfordern, nicht gut abschneiden. Ein klassisches Beispiel dafür, wo uni-modale Strategien versagen, ist ein Agent, der versucht, über einen See zu seinem Haus zu gelangen. Er kann nach Hause gelangen, indem er den See im Uhrzeigersinn (links) oder gegen den Uhrzeigersinn (rechts) umgeht, aber eine Gauß’sche Strategie ist nicht in der Lage, zwei Modi darzustellen. Stattdessen werden Aktionen aus einer Gaußschen Kurve ausgewählt, deren Mittelwert eine lineare Kombination der beiden Modi ist, was dazu führt, dass der Agent geradewegs in das eisige Wasser läuft. Traurig!

Das obige Beispiel veranschaulicht, wie die Normalverteilung zu vereinfachend sein kann. Zusätzlich zu den schlechten Symmetrieannahmen konzentriert sich die Dichte der Gauß-Verteilung in hohen Dimensionen größtenteils auf die Ränder und ist nicht robust gegenüber seltenen Ereignissen. Können wir eine bessere Verteilung mit den folgenden Eigenschaften finden?

1. Komplex genug, um reichhaltige, multimodale Datenverteilungen wie Bilder und Wertfunktionen in RL-Umgebungen zu modellieren?
2. … unter Beibehaltung der netten Eigenschaften einer Normalverteilung: Stichprobenziehung, Dichteauswertung und mit reparametrisierbaren Stichproben?

Die Antwort ist ja! Hier sind ein paar Möglichkeiten, dies zu tun:

• Verwendung eines Mischmodelles (siehe GMMs), um eine multimodale Policy zu repräsentieren, wobei eine kategorische Variable die “Option” und eine Mischung die Subpolicy repräsentiert. Auf diese Weise erhält man Stichproben, die einfach zu ziehen und auszuwerten sind. Es gibt aber ein Problem: Die Stichproben sind nicht trivial reparametrisierbar, was ihre Verwendung für VAEs und Posterior-Inferenz erschwert. Die Verwendung einer Gumbel-Softmax/Concrete Relaxierung der kategorischen “Option” würde jedoch eine multimodale, reparametrisierbare Verteilung liefern.
• Autoregressive Faktorisierungen von Policy-/Wertverteilungen. Insbesondere kann die kategorsche Verteilung jede diskrete Verteilung modellieren.
• In RL kann man dies ganz vermeiden, indem man die Symmetrie der Wertverteilung durch rekurrente Policies, Rauschen oder verteilungsbezogene RL bricht. Dies hilft, indem die komplexen Wertverteilungen in jedem Zeitschritt in einfachere bedingte Verteilungen zerlegt werden.
• Lernen mit energiebasierten Modellen, d.h. ungerichteten grafischen Modellen mit Potenzialfunktionen, die auf eine normalisierte probabilistische Interpretation verzichten. Hier ist ein Beispiel für diese Anwendung auf RL.
• Normalizing Flows: Hier lernen wir invertierbare, volumenverfolgende transformationen von Verteilungen, die wir leicht manipulieren können.

Sehen wir uns den letzten Ansatz an - Normalizing Flows.

Substitution und Volumenveränderung

Wir wollen eine gewisse Intuition entwickeln, indem wir die linearen Transformationen von 1D-Zufallsvariablen untersuchen. $X$ sei die Verteilung $Uniform(0,1)$. Sei die Zufallsvariable $Y=f(X)=2X+1$. $Y$ ist eine einfache affine Transformation (Skalierung und Verschiebung) der zugrundeliegenden “Ausgangsverteilung” $X$. Das bedeutet, dass eine Stichprobe $x_i$ aus $X$ in eine Stichprobe aus $Y$ umgewandelt werden kann, indem einfach die Funktion $f$ darauf angewendet wird.

Das grüne Quadrat stellt die schattierte Wahrscheinlichkeitsmasse auf $\mathbb{R}$ sowohl für $p(x)$ als auch für $p(y)$ dar - die Höhe stellt die Dichtefunktion bei diesem Wert dar. Da die Wahrscheinlichkeitsmasse für jede Verteilung zu 1 integriert werden muss, bedeutet die Skalierung des Bereichs durch 2 überall, dass wir die Wahrscheinlichkeitsdichte überall durch 2 teilen müssen, so dass die Gesamtfläche des grünen Quadrats und des blauen Rechtecks gleich ist (=1).

Zoomen wir auf ein bestimmtes $x$ und einen unendlich nahe gelegenen Punkt $x+dx$, so führt uns die Anwendung von $f$ auf diese beiden Punkte zu dem Paar $(y,y+dy)$.

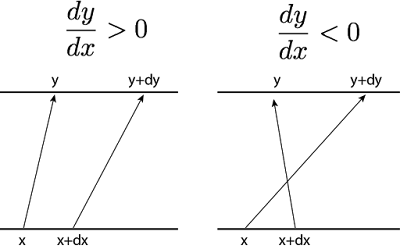
Auf der linken Seite haben wir eine lokal zunehmende Funktion $(dy/dx>0)$ und auf der rechten Seite eine lokal abnehmende Funktion $(dy/dx<0)$. Um die Gesamtwahrscheinlichkeit zu erhalten, muss die Änderung von $p(x)$ entlang des Intervalls $dx$ der Änderung von $p(y)$ entlang des Intervalls $dy$ entsprechen: $$p(x)dx=p(y)dy$$

Um die Wahrscheinlichkeit zu erhalten, interessiert uns nur der Betrag der Änderung von $y$ und nicht seine Richtung (es spielt keine Rolle, ob $f(x)$ bei $x$ zunimmt oder abnimmt, wir nehmen an, dass der Betrag der Änderung von $y$ in jedem Fall gleich ist). Daher ist $p(y)=p(x)\lvert dx/dy \rvert$. Im logarithmischen Raum ist dies gleichbedeutend mit $\log p(y)=\log p(x)+ \log \lvert dx/dy \rvert$. Die Berechnung von log-Dichten skaliert aus Gründen der numerischen Stabilität besser.

Betrachten wir nun den multivariablen Fall, mit 2 Variablen. Auch hier zoomen wir in einen unendlich kleinen Bereich unseres Gebiets und unser anfängliches “Segment” der Basisverteilung ist nun ein Quadrat mit der Breite $dx$.

Beachte, dass eine Transformation, die lediglich ein rechteckiges Feld $(x1,x2,x3,x4)$ verschiebt, die Fläche nicht verändert. Wir sind nur an der Änderungsrate pro Flächeneinheit von $x$ interessiert, daher kann die Verschiebung $dx$ als Maßeinheit betrachtet werden, die beliebig ist. Um die folgende Analyse einfach und einheitenlos zu gestalten, untersuchen wir ein Einheitsquadrat im Ursprung, d. h. 4 Punkte $(0,0),(1,0),(0,1),(1,1)$.

Durch Multiplikation mit der Matrix $[[a,b];[c,d]]$ werden die Punkte dieses Quadrats zu einem Parallelogramm, wie in der Abbildung rechts (unten) dargestellt. $(0,0)$ wird nach $(0,0)$ geschickt, $(1,0)$ nach $(a,b)$, $(1,0)$ nach $(c,d)$ und $(1,1)$ nach $(a+c,b+d)$.

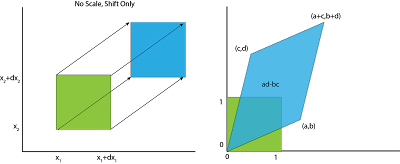
Ein Einheitsquadrat in der Domäne von $X$ entspricht also einem deformierten Parallelogramm in der Domäne von $Y$, sodass die Änderungsrate der Fläche pro Einheit die Fläche des Parallelogramms ist, d. h. ad-bc. Die Fläche eines Parallelogramms, ad-bc, ist nichts anderes als der Absolutwert der Determinante der linearen Transformation!

In drei Dimensionen wird die “Flächenänderung des Parallelogramms” zu einer “Volumenänderung des Parallelepipeds” und in noch höheren Dimensionen zu einer “Volumenänderung eines n-Parallelotops”. Das Konzept bleibt jedoch dasselbe - Determinanten sind nichts anderes als der Betrag (und die Richtung) der Volumenverzerrung einer linearen Transformation, verallgemeinert auf eine beliebige Anzahl von Dimensionen.

Was ist, wenn die Transformation $f$ nichtlinear ist? Anstelle eines einzigen Parallelogramms, das die Verzerrung eines beliebigen Punktes im Raum abbildet, kann man sich viele winzig kleine Parallelogramme vorstellen, die dem Betrag der Volumenverzerrung für jeden Punkt im Bereich entsprechen. Mathematisch gesehen ist diese lokal-lineare Änderung des Volumens $\lvert \det (J(f-1(x))) \rvert$, wobei $J(f^{-1}(x))$ die Jacobi-Matrix der inversen Funktion ist - eine höherdimensionale Verallgemeinerung der Größe $dx/dy$ von vorhin. $$y=f(x)$$ $$p(y)=p(f-1(y)) \lvert \det J(f-1(y)) \rvert$$ $$\log{p(y)}=\log{p(f-1(y))}+\log{\lvert \det(J(f-1(y))) \rvert}$$

Als ich in der Mittel- und Oberstufe etwas über Determinanten lernte, war ich sehr verwirrt über die scheinbar willkürliche Definition von Determinanten. Uns wurde nur beigebracht, wie man eine Determinante berechnet, statt zu wissen, was eine Determinante bedeutet: die lokale, linearisierte Rate der Volumenänderung einer Transformation (3Blue1Brown’s Videos hierzu sind absolut Gold wert!).

Transformierte Verteilungen in TensorFlow

TensorFlow hat eine elegante API zum Transformieren von Verteilungen. Eine TransformedDistribution wird durch ein Basisverteilungsobjekt spezifiziert, das wir transformieren werden, und ein Bijector-Objekt, das folgende Transformationen implementiert:

1. eine Vorwärtstransformation $y=f(x)$, wobei $f\colon \mathbb{R^d} \longrightarrow \mathbb{R^d}$
2. die inverse Transformation $x=f^{-1}(y)$, und
3. 3) die inverse log-Determinante des Jacobian $\log{\mid \det J(f^{-1}(y)) \mid}$ implementiert. Im weiteren Verlauf dieses Beitrags werde ich diese Größe mit ILDJ abkürzen.

Unter dieser Abstraktion ist das Vorwärtssampling trivial:

bijector.forward(base_dist.sample())

Um die log-Dichteverteilung der transformierten Verteilung auszuwerten:

distribution.log_prob(bijector.inverse(x)) + bijector.inverse_log_det_jacobian(x)

Wenn bijector.forward eine differenzierbare Funktion ist, dann ist Y = bijector.forward(x) eine reparametrisierbare Verteilung in Bezug auf die Stichproben x = base_distribution.sample(). Das bedeutet, dass normalisierende Flows als Ersatz für Variational Posteriors in einem VAE verwendet werden können (als Alternative zur häufig verwendeten Normalverteilung).

Einige häufig verwendete TensorFlow-Verteilungen sind tatsächlich mit diesen TransformedDistributions implementiert.

Ursprungsverteilung	Bijector.forward	Transformierte Verteilung
Normal	$exp(x)$	LogNormal
Exp(rate=1)	$-\log{x}$	Gumbel(0,1)
Gumbel(0,1)	$softmax(x)$	Gumbel-Softmax / Concrete

Gemäß der Standardkonvention werden transformierte Verteilungen als Bijector-1BaseDistribution bezeichnet; so wird ein ExpBijector, der auf eine Normalverteilung angewendet wird, zu LogNormal. Es gibt einige Ausnahmen von diesem Benennungsschema - die Gumbel-Softmax-Verteilung ist als RelaxedOneHotCategorical-Verteilung implementiert, die einen SoftmaxCentered-Bijektor auf eine Gumbel-Verteilung anwendet.

Normalizing Flows und das Lernen flexibler Bijektoren

Warum bei 1 Bijektor aufhören? Wir können eine beliebige Anzahl von Bijektoren miteinander verketten, ähnlich wie wir Schichten in einem neuronalen Netz miteinander verketten ³. Dieses Konstrukt wird als “Normalizing Flow” bezeichnet. Wenn ein Bijektor darüber hinaus über einstellbare Parameter in Bezug auf bijector.log_prob verfügt, kann der Bijektor tatsächlich so erlernt werden, dass er unsere Basisverteilung an beliebige Wahrscheinlichkeitsdichten anpasst. Jeder Bijektor fungiert als lernfähige “Schicht”, und man kann einen Optimierer verwenden, um die Parameter der Transformation zu lernen, damit sie zu der Datenverteilung passen, die man zu modellieren versucht. Ein Algorithmus hierfür ist die Maximum-Likelihood-Schätzung, die unsere Modellparameter so modifiziert, dass unsere Trainingsdatenpunkte eine maximale log-Wahrscheinlichkeit unter unserer transformierten Verteilung haben. Aus Gründen der numerischen Stabilität berechnen und optimieren wir eher über log-Wahrscheinlichkeiten als über Wahrscheinlichkeiten.

Diese Folie aus dem UAW-Vortrag von Shakir Mohamed und Danilo Rezende (Folien) veranschaulicht dieses Konzept:

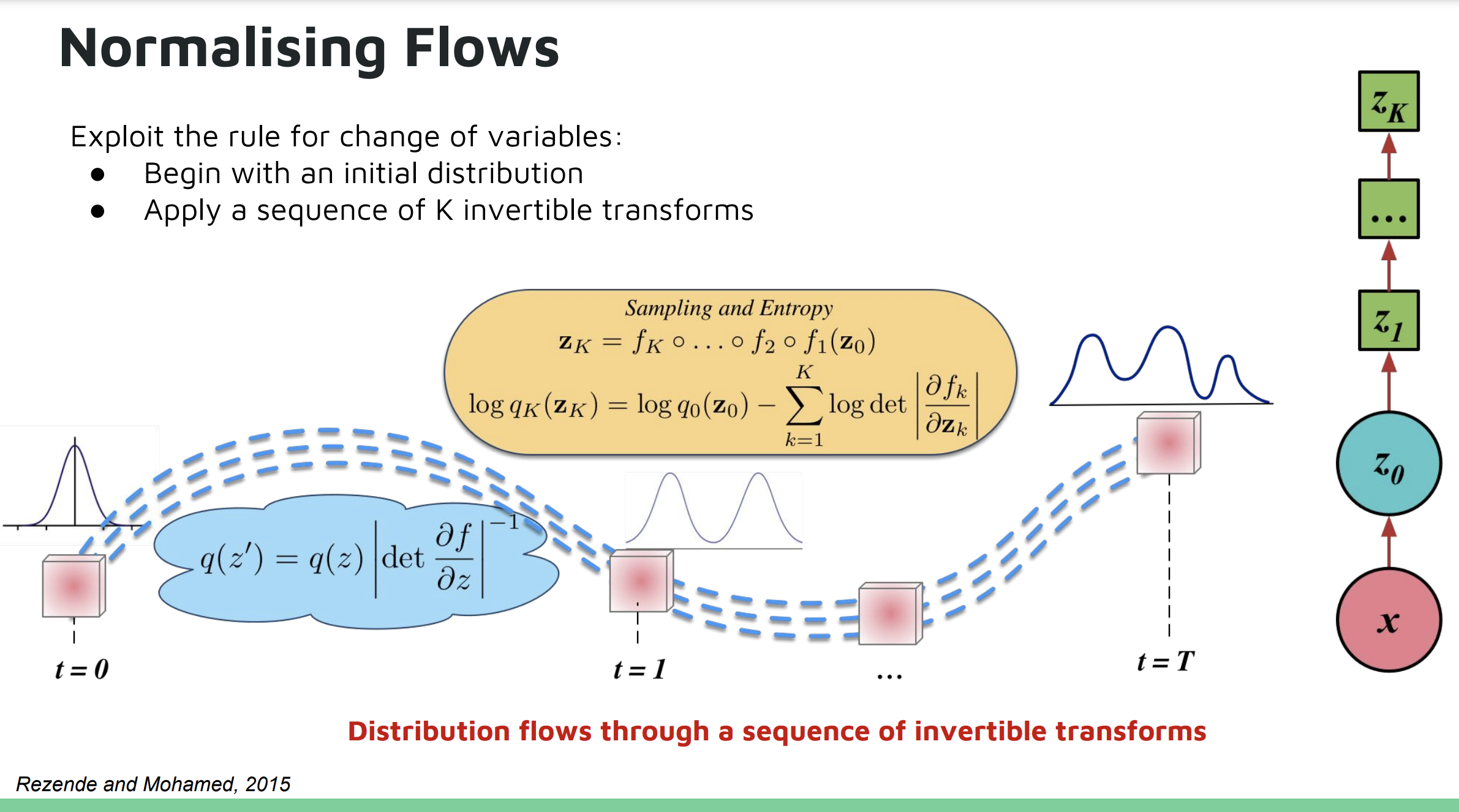
Die Berechnung der Determinante einer beliebigen N×N-Jacob-Matrix hat jedoch eine Laufzeitkomplexität von $O(N^3)$, was sehr teuer ist, wenn man sie in ein neuronales Netz einbaut. Hinzu kommt das Problem der Invertierung eines beliebigen Funktionsapproximators. Ein Großteil der aktuellen Forschung zu Normalizing Flows konzentriert sich darauf, wie ausdrucksstarke Bijectors entworfen werden können, die die GPU-Parallelisierung während der Vorwärts- und Umkehrberechnungen ausnutzen und gleichzeitig recheneffiziente ILDJs beibehalten.

Code-Beispiel

Lasst uns einen grundlegenden Normalizing Flow in TensorFlow in etwa 100 Zeilen Code erstellen. Dieses Codebeispiel wird Gebrauch machen von:

• TF Distributions - allgemeine API zur Manipulation von Verteilungen in TF. Für dieses Tutorial brauchst du TensorFlow 1.5 (s. Brad’s post für TensorFlow 2 Code).
• TF Bijector - allgemeine API zur Erstellung von Operatoren auf Verteilungen
• Numpy, Matplotlib.

# file: "nf1_imports.py"
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
tfd = tf.contrib.distributions
tfb = tfd.bijectors

Wir versuchen, die Verteilung $p(x_1,x_2)= \mathcal{N}(x_1 \mid \mu=1/4x_{2}^{2},\sigma=1) * \mathcal{N}(x_2 \mid \mu=0,\sigma=4)$ zu modellieren. Wir können Stichproben aus der Zielverteilung mit dem folgenden Codeschnipsel erzeugen (wir erzeugen sie in TensorFlow, um zu vermeiden, dass wir bei jedem Minibatch Stichproben von der CPU auf die GPU kopieren müssen):

# file: "nf1_target.py"
batch_size=512
x2_dist = tfd.Normal(loc=0., scale=4.)
x2_samples = x2_dist.sample(batch_size)
x1 = tfd.Normal(loc=.25 * tf.square(x2_samples),
                scale=tf.ones(batch_size, dtype=tf.float32))
x1_samples = x1.sample()
x_samples = tf.stack([x1_samples, x2_samples], axis=1)

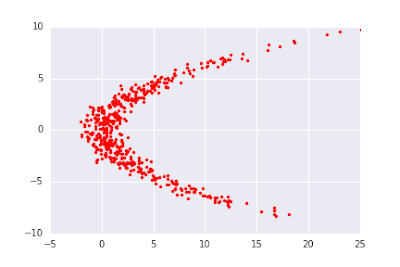
Für unsere Basisverteilung nutzen wir eine isotropische Normalverteilung:

# file: "nf1_base_dist.py"
base_dist = tfd.MultivariateNormalDiag(loc=tf.zeros([2], tf.float32))

Als Nächstes konstruieren wir den Bijector und erstellen daraus eine TransformedDistribution. Lasst uns einen flow aufbauen, der einem klassischen vollständig verbundenen Netzwerk ähnelt, d. h. alternierende Matrixmultiplikation und Nichtlinearitäten.

Die Jacobi-Matrix einer affinen Funktion ist trivial zu berechnen, aber im schlimmsten Fall sind die Determinanten $O(n^3)$, was inakzeptabel langsam ist. Stattdessen bietet TensorFlow eine strukturierte affine Transformation, deren Determinante effizienter berechnet werden kann. Diese affine Transformation ist parametrisiert als eine untere Dreiecksmatrix $M$ plus eine Aktualisierung niedrigen Ranges: $$M+V⋅D⋅V^T$$

Um $\det(M+V⋅D⋅V^T)$ kostengünstig zu berechnen, verwenden wir das Matrix-Determinanten-Lemma.

Nun benötigen wir eine invertierbare Nichtlinearität, um nichtlineare Funktionen auszudrücken (andernfalls bleibt die Kette der affinen Bijektoren affin). $Sigmoid$ / $tanh$ scheinen eine gute Wahl zu sein, aber sie sind unglaublich instabil zu invertieren - kleine Änderungen in der Ausgabe nahe -1 oder 1 entsprechen massiven Änderungen in der Eingabe. In meinen Experimenten konnte ich nicht 2 sättigende Nichtlinearitäten aneinanderreihen, ohne dass die Gradienten explodierten. $ReLU$ dagegen ist stabil, aber nicht invertierbar für $x<0$.

Ich entschied mich dafür, $PReLU$ (parametrisierte $ReLU$) zu implementieren, was dasselbe ist wie $Leaky ReLU$, aber mit einer lernbaren Steigung im negativen Bereich. Die Einfachheit von PReLU und seine simple Jacobi-Matrix sind eine gute Übung für die Implementierung eigener Bijektoren: Beachte, dass die ILDJ 0 ist, wenn $x>0$ (keine Volumenänderung) und $1/\alpha$ andernfalls (Kompensation der Volumenkontraktion durch Multiplikation von $x$ mit $\alpha$).

# file: "nf1_prelu.py"
# einfache Interpretation - Multiplikation mit alpha führt zur Volumenkontraktion
class LeakyReLU(tfb.Bijector):
    def __init__(self, alpha=0.5, validate_args=False, name="leaky_relu"):
        super(LeakyReLU, self).__init__(
            event_ndims=1, validate_args=validate_args, name=name)
        self.alpha = alpha

    def _forward(self, x):
        return tf.where(tf.greater_equal(x, 0), x, self.alpha * x)

    def _inverse(self, y):
        return tf.where(tf.greater_equal(y, 0), y, 1. / self.alpha * y)

    def _inverse_log_det_jacobian(self, y):
        event_dims = self._event_dims_tensor(y)
        I = tf.ones_like(y)
        J_inv = tf.where(tf.greater_equal(y, 0), I, 1.0 / self.alpha * I)
        # abs ist redundant hier, da det Jacobian > 0 hier
        log_abs_det_J_inv = tf.log(tf.abs(J_inv))
        return tf.reduce_sum(log_abs_det_J_inv, axis=event_dims)

PReLU ist eine elementweise Transformation, daher ist die Jacobi-Matrix diagonal. Die Determinante einer Diagonalmatrix ist einfach das Produkt der Diagonaleinträge, so dass wir die ILDJ durch einfache Summierung der Diagonaleinträge der log-Jacobi-Matrix ⁴ berechnen. Wir erstellen den “MLP Bijector” mit tfb.Chain() und wenden ihn dann auf unsere Basisverteilung an, um die transformierte Verteilung zu erhalten:

# file: "nf1_chain.py"
d, r = 2, 2
DTYPE = tf.float32
bijectors = []
num_layers = 6
for i in range(num_layers):
    with tf.variable_scope('bijector_%d' % i):
        V = tf.get_variable('V', [d, r], dtype=DTYPE)  # factor loading
        shift = tf.get_variable('shift', [d], dtype=DTYPE)  # affine shift
        L = tf.get_variable('L', [d * (d + 1) / 2],
                            dtype=DTYPE)  # lower triangular
        bijectors.append(tfb.Affine(
            scale_tril=tfd.fill_triangular(L),
            scale_perturb_factor=V,
            shift=shift,
        ))
        alpha = tf.abs(tf.get_variable('alpha', [], dtype=DTYPE)) + .01
        bijectors.append(LeakyReLU(alpha=alpha))
# Last layer is affine. Note that tfb.Chain takes a list of bijectors in the *reverse* order
# that they are applied.
mlp_bijector = tfb.Chain(
    list(reversed(bijectors[:-1])), name='2d_mlp_bijector')
dist = tfd.TransformedDistribution(
    distribution=base_dist,
    bijector=mlp_bijector
)

Zum Schluss trainieren wir das Modell mithilfe von Maximum-Likelihood-Schätzung: Maximierung der erwarteten log-Wahrscheinlichkeit unserer Stichproben von der realen Datenverteilung, gegeben unsere Modellwahl.

# file: "nf1_opt.py"
loss = -tf.reduce_mean(dist.log_prob(x_samples))
train_op = tf.train.AdamOptimizer(1e-3).minimize(loss)
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
NUM_STEPS = int(1e5)
global_step = []
np_losses = []
for i in range(NUM_STEPS):
    _, np_loss = sess.run([train_op, loss])
    if i % 1000 == 0:
        global_step.append(i)
        np_losses.append(np_loss)
    if i % int(1e4) == 0:
        print(i, np_loss)

Und das war’s! TensorFlow-Distributionen machen Normalizing Flows implementierbar und akkumulieren automatisch alle Jacobi-Determinanten in einer Weise, die sauber und gut lesbar ist. Der vollständigen Code findet könnt ihr auf Github finden.

Ihr werdet vielleicht festellen, dass die Deformation ziemlich langsam ist und dass es viele Schichten braucht, um eine relativ einfache Transformation zu lernen ⁵. Im nächsten Post werde ich modernere Techniken zum Erlernen von Normalizing Flows behandeln.

Credits

Vielen Dank an Eric Jang für ein cooles Tutorial und die Möglichkeit, es deutschen Lesern zugänglich zu machen! Außerdem vielen Dank an Brad Saund, dessen Blogpost ähnliche Beispiele zu den obigen in TensorFlow2 enthält!

Photo by JJ Ying on Unsplash

1. Die Vorstellung, dass wir unseren Datensatz mit *neuen* Informationen aus einem endlichen Datensatz erweitern können, ist ziemlich beunruhigend, und es muss sich erst noch zeigen, ob probabilistisches maschinelles Lernen wirklich echte generative Prozesse ersetzen kann (z. B. die Simulation der Flüssigkeitsdynamik), oder ob es am Ende des Tages nur zur Amortisierung von Berechnungen taugt und jede Verallgemeinerung, die wir über die Trainings-/Testverteilung erhalten, ein glücklicher Zufall ist. ↩︎

2. A note on the evaluation of generative models ist eine anregende Diskussion darüber, dass eine hohe log-likelihood weder ausreichend noch notwendig ist, um “plausible” Bilder zu erzeugen. Dennoch ist es besser als nichts und in der Praxis ein nützliches Diagnoseinstrument. ↩︎

3. Es gibt eine Verbindung zwischen Normalizing Flows und GANs über Encoder-Decoder-GAN-Architekturen, die die Inverse des Generators lernen (ALI / BiGAN). Da es einen separaten Encoder gibt, der versucht, $u=G^{-1}(X)$ so wiederherzustellen, dass $X=G(u)$ ist, kann man sich den Generator als einen Flow für die einfache uniforme Verteilung vorstellen. Wir wissen jedoch nicht, wie wir den Betrag der Volumenexpansion/-kontraktion in Bezug auf $X$ berechnen können, so dass wir die Dichte nicht aus GANs gewinnen können. Es ist jedoch wahrscheinlich nicht völlig unvernünftig, die log-det-Jacobimatrix numerisch zu modellieren oder eine Art von Linearzeit-Jacobimatrix durch Konstruktion zu erzwingen. ↩︎

4. Das Lemma “Die Determinante einer Diagonalmatrix ist das Produkt der Diagonaleinträge” ist aus geometrischer Sicht recht intuitiv: Die Längenverzerrung jeder Dimension ist unabhängig von den anderen Dimensionen, so dass die gesamte Volumenänderung nur das Produkt der Änderungen in jeder Richtung ist, als ob wir das Volumen eines hochdimensionalen rechteckigen Prismas berechnen würden. ↩︎

5. Die Kapazität dieses MLP ist eher begrenzt, da jede affine Transformation nur eine 2x2-Matrix ist und PReLU die zugrunde liegende Verteilung nur sehr langsam “verformt” (daher sind mehrere PreLUs erforderlich, um die Daten in die richtige Form zu bringen). Für niedrigdimensionale Verteilungen ist dieses MLP eine sehr schlechte Wahl für einen Normalizing Flow und ist zur Illustration der Konzepte gedacht. ↩︎