How does Pytorch implement a linear layer?

How to find the implementation of a PyTorch operator - A whirlwind tour
PyTorch is the deep learning library. It is used by researchers and practitioners alike to build and train neural networks. It is also open source, which means that we can look at the source code to understand how it works. This is especially useful if we want to understand how a specific operation is implemented.
In my post about GPU programming in PyTorch, we saw that calling a linear layer in PyTorch via torch.nn.Linear results in a call to the aten::addmm function. The ATen library is part of the PyTorch C++ API and is responsible for the tensor operations in PyTorch. So if we want to understand how the linear layer is implemented in PyTorch, we need to dig into C++ code and understand how the aten::addmm function is implemented. This is a bit of a convoluted process, but I hope that in the process you learn as much about the PyTorch codebase as I did when I went down this rabbit hole.
- PyTorch Docs and the Dispatcher
- Native functions and the codegen pipeline
- Navigating the
at::nativenamespace - Structured Kernels
- Where are the actual implementations?
- Conclusion
- Credits
PyTorch Docs and the Dispatcher
To get an idea of what these operations do, we can look at the PyTorch at Namespace docs and look for these functions. Via this we see that the aten::addmm function is defined in build/aten/src/ATen/Functions.h. Looking at the program listing, we can see that it calls at::_ops::addmm_out::call(self, mat1, mat2, beta, alpha, out).
We can look at the respective Python API to learn more about the different arguments of the addmm function. The addmm function is a matrix multiplication followed by a matrix addition of the following form:
The mat1 and mat2 arguments are the input matrices, beta is a scaling factor for the input matrix input, alpha is a scaling factor for the matrix multiplication and out is the output tensor.
Just looking through the PyTorch GitHub repo looking for the implementation of function is unfortunately quite a pain. One of the main reasons for that is that depending on your backend (CPU, NVIDIA GPU, Apple M-series chips, …), the PyTorch dispatcher dynamically dispatches to the correct kernel for your setup.
Native functions and the codegen pipeline
Another complication is that many operations are not really fully implemented in the PyTorch codebase, but will get generated during the PyTorch build process via a code-generation pipeline (more on this in this podcast episode). This is sensible since while many operations in PyTorch are in principle quite simple (element-wise additions, activation functions, …), there is a lot of boilerplate that every operation has to implement (like bindings to python, autograd support, registering the kernel to the dispatcher, …). The codegen pipeline allows PyTorch to generate this boilerplate code automatically.
What we need to do therefore is to look at the native_functions.yaml file, with “native” functions being the modern mechansim for adding operators and functions to ATen (more details in this podcast episode). This file describes metadata about each operator that gets consumed by the codegen (more details on the different fields in this yaml file here).
If we search in the native_functions.yaml file for addmm, we find the following entry:
# file: "native_functions.yaml"
- func: addmm(Tensor self, Tensor mat1, Tensor mat2, *, Scalar beta=1, Scalar alpha=1) -> Tensor
structured_delegate: addmm.out
variants: function, method
dispatch:
SparseCPU: addmm_sparse_dense_cpu
SparseCUDA: addmm_sparse_dense_cuda
SparseCsrCPU, SparseCsrCUDA: addmm_sparse_compressed_dense
tags: core
Entry for the addmm function
We see the structured_delegate field, which tells us that the actual implementation of the addmm function is in the addmm.out function (more on this later). We can find the implementation of this function in the native_functions.yaml file:
# file: "native_functions.yaml"
- func: addmm.out(Tensor self, Tensor mat1, Tensor mat2, *, Scalar beta=1, Scalar alpha=1, Tensor(a!) out) -> Tensor(a!)
structured: True
dispatch:
CPU: addmm_out_cpu
CUDA: addmm_out_cuda
MPS: addmm_out_mps
SparseCPU: addmm_out_sparse_dense_cpu
SparseCUDA: addmm_out_sparse_dense_cuda
SparseCsrCPU: addmm_out_sparse_compressed_cpu
SparseCsrCUDA: addmm_out_sparse_compressed_cuda
Entry for the addmm function
Ignoring the structured field for now, we see multiple things:
- We have multiple entries for the
addmmfunction,addmmandaddmm_out. There are in fact three different versions of most PyTorch operators (however, we only see theaddmmandaddmm_outfunctions in the codebase since the in-place version is generated automatically):addmm: the functional version that performs the operation without modifying the original tensor and returns a new tensor, for exampleoutput = torch.add(input, other)addmm_: the in-place version that modifies the original tensor, for exampleinput.add_(other)addmm_out: the out-of-place version that takes an additional tensor as an argument and writes the result to this tensor, for exampletorch.add(input, other, out=output)
We see that for each backend (CPU, CUDA, MPS, …) there is a separate implementation of the
addmmfunction. This is because the implementation of theaddmmfunction can be highly dependent on the specific hardware and memory layout of the input tensors. For example, theaddmmfunction for sparse tensors is implemented differently than theaddmmfunction for dense tensors.In summary, this means that we need to write (#variants * #backends kernel) implementations for each operator. This is a lot of boilerplate code that the codegen pipeline can generate for us.
- The
variantsfield tells us that theaddmmfunction can be called as a namespace function (at::addmm()) or as a Tensor method (t.addmm()). This is because PyTorch supports both functional and method-based APIs. To qualify as a Tensor method, there most be aTensor selfargument in the function signature since otherwise the function would not be able to be called as a method on a tensor. In the method variant this argument will be removed from the function signature. A function variant is always generated by ATen, but when should you also generate a method variant? From the PyTorch native README:
Tensor operations as methods are appropriate for “core” Tensor operations (e.g., add, sub, etc.), but not for more complicated neural network layers (e.g.,
conv2d) and internal functions designed specifically for binding (e.g.,cudnn_convolution).
Navigating the at::native namespace
If we want to look for where a specific implementation of the addmm function is, we just need to look for the name of the function in the at::native namespace. This still does not bring us to the actual implementation of the function easily because there are more than 2000 PyTorch operators which can be grouped into various categories. We can see in the post linked in the last sentence that addmm is counted as one of the 13 composite matmul operators. There are different ways to categorize the operators (for example by shape behavior), but the point is that there are a lot of them.
To find our addmm needle in the at::native namespace haystack, we can either directly open a codespace on GitHub or we can clone the PyTorch repo. Both options give us access to a terminal where we can find the implementation of the addmm function by running git grep "addmm". This will give us a list of all files in the current folder of the PyTorch repo that contain the string addmm. We can then look through these files to find the actual implementation of the addmm function. So we do the following in summary:
git clone https://github.com/pytorch/pytorch
cd pytorch/aten/src/ATen/native
git grep "addmm"
This gives us a lot of output, but we can see that there are two kinds of functions declarations in LinearAlgebra.cpp that look promising:
- A meta function called
TORCH_META_FUNC(addmm) - Multiple implementatin functions:
TORCH_IMPL_FUNC(addmm_out_cpu), but also the CUDA implementation in thecuda/Blas.cppfile calledTORCH_IMPL_FUNC(addmm_out_cuda)
This insight leads us to another new term we have to understand in order to make sense of the codebase: Structured Kernels.
Structured Kernels
Structured Kernels is a new (i.e. from 2021) way to define PyTorch operators. It abstracts away even more of the boilerplate code that has to be written for each operator and backend than native functions alone, to the extent that you only need to write a shape-checking function (meta function) and a kernel implementation function for the out-kernel and the structured kernel will take care of the rest.
This now explains the structured and structured_delegate fields in the native_functions.yaml file. The structured field tells us that the addmm function is a structured kernel, and the structured_delegate field tells us that the actual implementation of the addmm function is in the addmm.out function.
Pre structured kernels, entries in the native_functions.yaml file looked like this:
# file: "native_functions.yaml"
- func: addmm(Tensor self, Tensor mat1, Tensor mat2, *, Scalar beta=1, Scalar alpha=1) -> Tensor
# structured_delegate: addmm.out removed!
variants: function, method
dispatch:
#CPU, CUDA and MPS kernels added!
CPU: addmm_cpu
CUDA: addmm_cuda
MPS: addmm_mps
SparseCPU: addmm_sparse_dense_cpu
SparseCUDA: addmm_sparse_dense_cuda
SparseCsrCPU, SparseCsrCUDA: addmm_sparse_compressed_dense
tags: core
# file: "native_functions.yaml"
- func: addmm.out(Tensor self, Tensor mat1, Tensor mat2, *, Scalar beta=1, Scalar alpha=1, Tensor(a!) out) -> Tensor(a!)
# structured: True removed!
dispatch:
CPU: addmm_out_cpu
CUDA: addmm_out_cuda
MPS: addmm_out_mps
SparseCPU: addmm_out_sparse_dense_cpu
SparseCUDA: addmm_out_sparse_dense_cuda
SparseCsrCPU: addmm_out_sparse_compressed_cpu
SparseCsrCUDA: addmm_out_sparse_compressed_cuda
You see that before structured kernels, both the addmm and addmm_out functions had a dispatch field that specified all the backends for which the function had to be implemented. The CPU, CUDA and MPS kernel now have to be implemented separately for the addmm and addmm_out functions. This is a lot of boilerplate code that the structured kernel can generate for us.
In the structured kernel yaml file, you see that the addmm function has a structured_delegate field that points to the addmm.out function. This is because the addmm function is a structured kernel, and the actual implementation of the addmm function is in the addmm.out function. The addmm.out function is a structured kernel that is implemented in the LinearAlgebra.cpp file.
In the ideal case of a structured kernel, the addmm function would not need any dispatch field because the addmm_out as the structural delegate would implement all the kernel implementations. This can be seen in the example from the RFC for structured kernels:
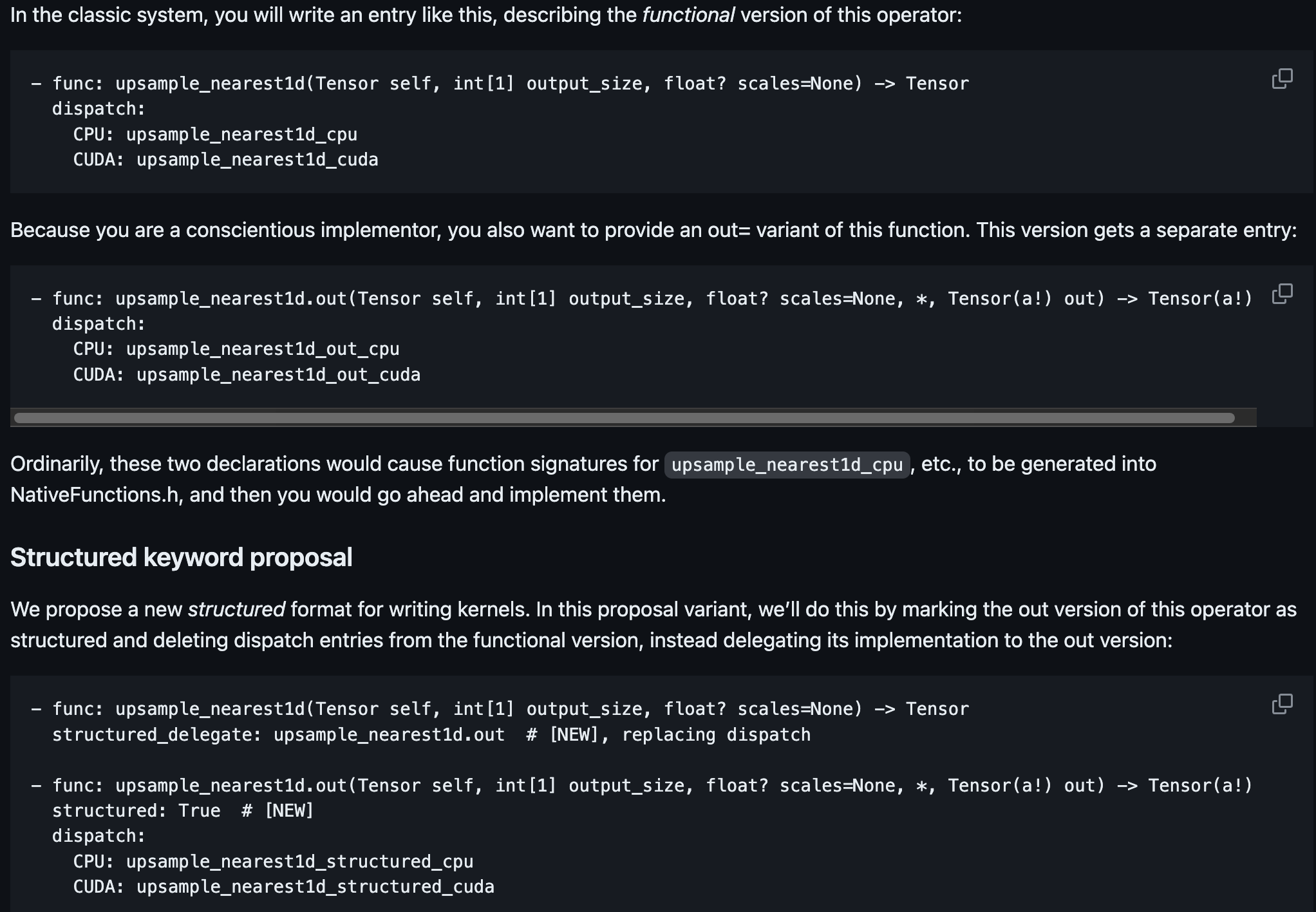
In the addmm function, however, we still see the dispatch field. This is because the addmm function is a composite matmul operator, and the implementation can be highly specific in the sparse case. Therefore we cannot rely on the structured kernel to generate the correct implementation for us, and we have to specify the dispatch field manually. If you want to learn more about how all this is implemented under the hood, check out this slide deck.
Where are the actual implementations?
We are already quite deep down in the rabbit hole and tracked down the addmm function to the LinearAlgebra.cpp and the cuda/Blas.cpp file. These files contains the meta function TORCH_META_FUNC(addmm) and the implementation functions TORCH_IMPL_FUNC(addmm_out_cpu) and TORCH_IMPL_FUNC(addmm_out_cuda). The TORCH_META_FUNC function is a meta function that checks the shapes of the input tensors and calls the correct implementation function. The TORCH_IMPL_FUNC function is the actual implementation of the addmm function for the CPU and CUDA backends.
Let us look at these in turn now.
Shape checking: TORCH_META_FUNC(addmm)
The TORCH_META_FUNC(addmm) function is a wrapper around ADDMM_META(). Why another wrapper, you may ask? Well, the shape checkign done is this function is transferable to other cases such as for TORCH_META_FUNC(_addmm_activation), so the wrapper promotes reusability.
Looking at the implementation of ADDMM_META(), we see that it is actually not a function but a preprocessor macro:
#define ADDMM_META() \
TORCH_CHECK(self.scalar_type() == mat2.scalar_type(), "self and mat2 must have the same dtype, but got ", self.scalar_type(), " and ", mat2.scalar_type()); \
TORCH_CHECK(mat1.scalar_type() == mat2.scalar_type(), "mat1 and mat2 must have the same dtype, but got ", mat1.scalar_type(), " and ", mat2.scalar_type()); \
TORCH_CHECK(mat1.dim() == 2, "mat1 must be a matrix, got ", mat1.dim(), "-D tensor"); \
TORCH_CHECK(mat2.dim() == 2, "mat2 must be a matrix, got ", mat2.dim(), "-D tensor"); \
TORCH_CHECK( \
mat1.sizes()[1] == mat2.sizes()[0], "mat1 and mat2 shapes cannot be multiplied (", \
mat1.sizes()[0], "x", mat1.sizes()[1], " and ", mat2.sizes()[0], "x", mat2.sizes()[1], ")"); \
\
auto names = at::namedinference::propagate_names_for_addmm(mat1, mat2, self); \
set_output_raw_strided(0, {mat1.sizes()[0], mat2.sizes()[1]}, {}, mat1.options(), names);
As expected, it performs a lot of checks on the input tensors. It checks that the input tensors have the same data type, that mat1 and mat2 are both 2D tensors (i.e. matrices), and that the shapes of mat1 and mat2 are compatible for matrix multiplication. It then calls the at::namedinference::propagate_names_for_addmm function to propagate the names of the input tensors to the output tensor. Finally, it sets the output tensor to the correct shape.
CPU implementation: TORCH_IMPL_FUNC(addmm_out_cpu)
If we look at the TORCH_IMPL_FUNC(addmm_out_cpu) function, we see that it is again a wrapper! It first expands the output tnesor to the correct shape (rows = {mat1.sizes()[0], columns = mat2.sizes()[1]}) and then calls the addmm_impl_cpu_() function.
Fortunately, this time we do not have to search long for the actual implementation of the addmm_impl_cpu_() function. It is in the same file and longer than the previous wrapper function (which makes sense since it is the actual implementation of the addmm function).
Looking at the function signature, we see the following:
static void addmm_impl_cpu_(
Tensor &result, const Tensor &self, Tensor m1, Tensor m2, const Scalar& beta, const Scalar& alpha)
We see that the function does not return anything, but takes a reference to the output tensor result and the input tensors self, m1 and m2 as well as the scaling factors beta and alpha. It starts with a some shape asserts and data type checks. It then allocates the sizes of the different matrices to auto variables since accessing these arrays is faster than calling the size() method multiple times (we will need these sizes for the matrix multiplication). After some additional checks and resizings we get to the core of the function.
// Some paths in the code below do not handle multiplications of the form [a, 0] x [0, b]
if (m1_sizes[1] == 0) {
if (beta.toComplexDouble() == 0.0) {
result.zero_();
} else {
if (!self.is_same(result)) {
result.copy_(self);
}
result.mul_(beta);
}
return;
}
Checks for the value. Link
As the comment tells us, the code after the excerpt cannot handle multiplications of the form , so it checks for this case and handles it separately. We can see that if the input scaling factor is zero, the output tensor is zeroed out. If the input scaling factor is not zero, the output tensor copies the entries from the self tensor and is scaled by . The function then returns.
After that, we cast the tensors result and m1 as matrix a and m2 as matrix b. We do this to prepare the shapes correctly for the matrix multiplication.
Finally, we get to the matrix multiplication itself. Depending on which CPU hardware we have we can still dispatch to two different implementation.
- On AArch64 we can call the
mkldnn_matmulfunction that is faster in case certain shape considerations are fulfilled:
bool dispatched = false;
#if defined(__aarch64__) && AT_MKLDNN_ACL_ENABLED()
// On AArch64 if LHS matrix in BLAS routine is transposed but RHS is not then
// it is faster to call oneDNN matrix multiplication primitive with RHS*LHS
// that will call then into Arm® Compute Library (ACL) GEMM kernel and also
// additionally have support for running kernel with BF16 instructions
if (transpose_c) {
bool apply_heur = apply_mkldnn_matmul_heur(b.sizes()[0], b.sizes()[1], a.sizes()[1]);
if (apply_heur && transpose_a && !transpose_b && result.scalar_type() == at::ScalarType::Float) {
try {
mkldnn_matmul(b, a, c, beta.to<float>(), alpha.to<float>());
// We have dispatched to ACL GEMM for single precision float
// so do not need to dispatch to BLAS GEMM below
dispatched = true;
} catch (const std::exception& e) {
TORCH_WARN("mkldnn_matmul failed, switching to BLAS gemm:", e.what());
at::globalContext().setUserEnabledMkldnn(false);
}
}
}
#endif
AArch64 matrix multiplication dispatch. Link
- If this option is not enabled (or if the heuristic check for the matrix shapes fails), we fall back to the
gemmfunction from the BLAS library:
if(!dispatched) {
// Apply BLAS routine
_AT_DISPATCH_ADDMM_TYPES(result.scalar_type(), "addmm_impl_cpu_", [&]{
using opmath_t = at::opmath_type<scalar_t>;
at::native::cpublas::gemm(
transpose_a ? a.is_conj() ? TransposeType::ConjTranspose : TransposeType::Transpose : TransposeType::NoTranspose,
transpose_b ? b.is_conj() ? TransposeType::ConjTranspose : TransposeType::Transpose : TransposeType::NoTranspose,
m, n, k,
alpha.to<opmath_t>(),
a.const_data_ptr<scalar_t>(), lda,
b.const_data_ptr<scalar_t>(), ldb,
beta.to<opmath_t>(),
c.mutable_data_ptr<scalar_t>(), ldc);
});
}
CPU BLAS dispatch to the GEMM function. Link
With this, we have the actual implementation of the addmm function for the CPU backend.
CUDA implementation: TORCH_IMPL_FUNC(addmm_out_cuda)
The CUDA implementation is quite similar on first sight: we again call the actual implementation function addmm_out_cuda_impl() which is reused in multiple other functions.
The actual implementation of the addmm_out_cuda_impl() function is in the same file and again starts with some shape asserts and data type checks. We again have some a check that looks at the case where the input scaling factor is zero and handles it separately:
if (mat1.numel() == 0) {
// By definition, when beta==0, values in self should be ignored. nans and infs
// should not propagate
if (beta.toComplexDouble() == 0.) {
return result.zero_();
}
// TODO: We could squeeze some perf by calling at::cuda::mul_out here instead, to bypass the dispatcher.
// That requires some fixing some internal build dependencies though.
return at::mul_out(
result,
self.expand(result.sizes()),
at::native::scalar_tensor(
beta,
self.scalar_type(),
c10::nullopt /* layout */,
at::kCPU,
c10::nullopt /* pin_memory */));
}
checks of the addmm CUDA implementation. Link
After that, we again dispatch to different kernels (this time CUDA kernels) depending on the hardware we have. The CUDA implementation is more complex than the CPU implementation since we have to take into account the different CUDA hardware architectures and the different CUDA libraries that are available. Here is one example:
// If batch is 1 call gemm rather than bgemm
if (num_batches == 1) {
at::cuda::blas::gemm<scalar_t>(
transa, transb,
m, n, k,
alpha_val,
batch1_ptr, lda,
batch2_ptr, ldb,
beta_val,
result_ptr, ldc);
} else {
at::cuda::blas::bgemm<scalar_t>(
transa, transb,
m, n, k,
alpha_val,
batch1_ptr, lda, batch1_->strides()[0],
batch2_ptr, ldb, batch2_->strides()[0],
beta_val,
result_ptr, ldc, result_->strides()[0],
num_batches
);
}
CUDA GEMM dispatch. Link
You can see that depending on the number of batches, we call either the gemm or the bgemm function from the CUDA BLAS library. The bgemm function is a batched version of the gemm function that can perform multiple matrix multiplications in parallel. This is useful if we have a batch of matrices that we want to multiply with the same matrix mat2. To learn more about the different CUDA BLAS functions, you can look at the cuBLAS documentation and the matrix multiplication user guide.
Conclusion
In this post, we went on a whirlwind tour of the PyTorch codebase to understand how the addmm function is implemented. We saw that the addmm function is not only a PyTorch native function specified in the native_functions.yaml file, but also a structured kernel and that the actual implementation of the addmm function is in the addmm.out function. We then looked at the addmm.out function and realised that it is a wrapper around the addmm_impl_cpu_() and addmm_impl_cuda_() functions. Upon inspecting the addmm_impl_cpu_() and addmm_impl_cuda_() it became clear that these are the actual implementations of the addmm function for the CPU and CUDA backends and look quite complicated to to different dispatch conditions, shape checks and data type checks, but the core of the function (the matrix multiplication) in the end is again a call to a kernel from a library.
I hope that this post gave you a good overview of how to find the implementation of a PyTorch operator and how to navigate the PyTorch codebase. If you have a better way to do that, let me know!
Credits
There is an amazing blog post about PyTorch internals by Ed Zang as well as his PyTorch developer podcast that helped me immensely in understanding the PyTorch codebase. Also shoutout to Christian Perone for his slides on PyTorch 2 internals that shine some light on the recent developments connected with the PyTorch 2 release.
PyTorch Logo taken from this post.
